SOAL BENTUK ALJABAR, SUKU SEJENIS dan tak sejenis

Tentukanlah nilai koefisien y dari bentuk – bentuk aljabar berikut ini!
a. 5x^2 + 6y – 7
b. 3x^2 – 4py + 2y2
c. 3/5y^2 + 2/3y – 5Tentukan suku-suku yang sejenis pada bentuk aljabar berikut ini.A. 9k+8m-4km-15k+7km
B. 7p²-8p²q-11p²+p²q+12pq²

2. Sederhanakan bentuk-bentuk aljabar sebagai berikut.
A.5x-3x
B.9+4x-1
C.4x+8x+12
D. 7-2x-x+5
E.3x²+3y²,5xy+2x²-5y²+6xy

BENTUK ALJABAR KELAS 7 KURIKULUM 2013 (Pengertian aljabar, dan unsur-unsur bentuk aljabar)

A. Pengertian Bentuk Aljabar

Pada operasi perkalian bilangan bulat, telah dibahas arti perkalian dua bilangan bulat sbb:

2 x 8 = 8 + 8 -----------> Jumlah delapanan terdiri atas dua suku.

5 x 3 = 3 + 3 + 3 + 3 + 3 -----------> Jumlah tigaan terdiri atas lima suku

Berdasarkan pada arti perkalian di atas , dapat diuraikan perngertian bentuk  aljabar sbb:

4 x a = a + a + a +a = 4a

6 x b = b + b + b + b + b +b = 6b

bentuk-bentuk seperti  4a, 6a, 3x + 4 disebut bentuk aljabar.

Bentuk Aljabar merupakan bentuk operasi atau pengerjaan hitung yang terdiri dari satu atau beberapa suku yang melibatkan peubah atau variabel.

Unsur-unsur bentuk aljabar :

•     Variabel : lambang pada bentuk aljabar yang dinyatakan dengan huruf kecil yang dipisahkan oleh operasi penjumlahan atau pengurangan

•     Koefisien : lambang (bilangan) yang memuat suatu variabel atau pengali suatu variabel

•     Konstanta : bilangan yang tidak memuat suatu variabel

•     Factor : bagian dari suatu hasil kali

•     Suku : bagian dari bentuk aljabar yang dipisahkan oleh operasi hitung Suku memiliki dua jenis, yaitu :

a.Suku Sejenis adalah suku-suku dalam bentuk aljabar yang mempunyai      variabel yang sama, sehingga dapat dijumlahkan atau dikurangkan.
b.Suku Tak Sejenis adalah suku-suku dalam bentuk aljabar yang mempunyai variabel yang berbeda

LATIHAN SOAL PERSAMAAN GARIS LURUS KELAS 8 KURIKULUM 2013

Berikut kami sampaikan latihan soal Persamaan Garis Lurus Kelas 8

1. Bentuk-bentuk berikut yang merupakan persamaan garis lurus adalah............

a. x + y = 0

b. 2y - x + 1

c. x + y - 2

d. y = 2 + 5

2. Garis-garis berikut yang melalui titik pusat koordinat adalah.........

a. 2x + y = 0

b. 2x - y = 6

c. 3x - 2y + 12 = 0

d. y = 5x - 10

3. Persamaan garis yang melalui titik-titik (1, 2), ( 3, 6), (-4, -8) adalah............

a. 2y = x

b. y = 2x

c. 3y = 9x

d. 5y = 12x

4. Persamaan garis lurus yang bergradien m = -1 dan melalui P(4, -1) adalah........

a. y + x = 3

b. y - x = 3

c. y + x = -3

d. y - x = -3

5. Persamaan garis lurus yang melalui (-3, -5) dengan gradien m = -2 adalah........

a. 2x - y - 11 = 0

b. 2x - y + 11 = 0

c. 2x + y - 11 = 0

d. 2x + y + 11 = 0

RELASI DAN FUNGSI MATEMATIKA KELAS 8

MATERI RELASI DAN FUNGSI

MATEMATIKA SMP KELAS VIII K-13

A. Relasi

1. Pengertian Relasi
Relasi adalah hubungan antara anggota suatu himpunan dengan anggota himpunan yang lain. Relasi dari himpunan A ke himpunan B adalah menghubungkan anggota-anggota himpunan A dengan anggota-anggota himpunan B.
Contoh:
Himpunan A ={1,2,3} dan B={A,B,C}. Anggota-anggota himpunan A dan B dapat dihubungkan dengan relasi yaitu "faktor dari".
2. Cara menyatakan Relasi
Cara menyatakan Relasi dapat dilakukan dengan:
a. Diagram Panah
Contoh di atas dapat dinyatakan dengan diagram panah sbb:

b. Diagram Cartesius
Contoh di atas dapat dinyatakan dengan diagram panah sbb:

c. Himpunan Pasangan Berurutan
Contoh di atas dapat dinyatakan dalam himpunan pasangan berurutan dengan memasangkan secara berurutan anggota-anggota himpunan A dan anggotaanggota himpunan B yaitu:
{(1,A), (1,B), (2,B), (3,B), (3,C)}

B. Fungsi (Pemetaan)

1. Pengertian Fungsi (pemetaan)
Fungsi dari himpunan A ke himpunan B merupakan relasi yang menghubungkan setiap anggota himpunan A ke tepat satu anggota himpunan B.
Contoh Pemetaan/Fungsi:

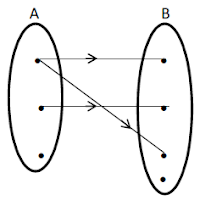
Contoh Bukan Pemetaan/Fungsi:

Tidak semua anggota himpunan A dihubungkan dengan anggota himpunan B.

2. Domain, Kodomain dan Range
Domain = daerah asal
Kodomain = daerah kawan
Range = daerah hasil

Himpunan A={1,2,3} disebut domain
Himpunan B={A,B,C} disebut kodomain
Hasil pemetaan yaitu {A,B} disebut range

3. Banyaknya Fungsi
Jika banyaknya anggota himpunan A adalah n(A) dan banyaknya anggota himpunan B adalah n(B) maka:
Banyaknya fungsi yang mungkin dari A ke B = n(B)^n(A)
Banyaknya fungsi yang mungkin dari B ke A = n(A)^n(B)

Contoh:
Himpunan A ={1,2,3,4} dan B={A,B,C}, carilah:
a. Banyaknya fungsi yang mungkin dari A ke B
b. Banyaknya fungsi yang mungkin dari B ke A
Jawab:
Diketahui:
n(A) = 4 dan n(B) = 3
a. Banyaknya fungsi yang mungkin dari A ke B = n(B)^n(A) = 34 = 81
b. Banyaknya fungsi yang mungkin dari B ke A = n(A)^n(B) = 43 = 64

4. Notasi dan Rumus Fungsi Linear
a. Notasi fungsi linear
Fungsi linear dinotasikan dengan f : x → ax + b
dimana:
f = nama fungsi
x = anggota daerah asal
ax+ b = bayangan dari x

b. Rumus fungsi linear
f(x) = ax + b
x variabel dan f(x) nilai fungsi
contoh:
f(x) = 2x + 2
Nilai fungsi untuk x = 2 adalah f(2) = 2 x 2 + 2 = 6

c. Grafik fungsi linear
Contoh: 
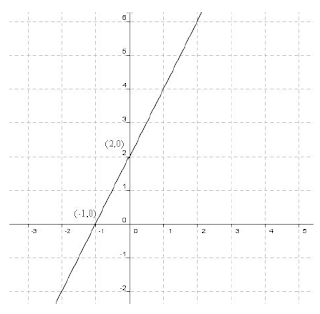
gambarlah grafik fungsi f(x) = 2x + 2
jawab:
tentukan titik potong dengan sumbu x dan y terlebih dahulu:
titik potong dengan sumbu x jika f(x) = 0
0 = 2x + 2 → 2x = -2, maka x = -1
diperoleh titik (-1,0)
titik potong dengan sumbu y jika x = 0
f(x) = 2x + 2  f(x) = 2. 0 + 2 = 2
diperoleh titik (0,2)
Buat sumbu koordinat dengan titik-titik (-1,0) dan (0,2) tersebut, kemudian
tarik garis lurus yang melewati titik-titik koordinat tersebut.

5. Korespondensi Satu-satu
Suatu fungsi disebut korespondensi satu-satu jika setiap anggota A tepat berpasangan dengan setiap anggota B.

Banyaknya korespondensi satu-satu yang mungkin antara himpunan A dan B adalah:
1 x 2 x 3 x .......x(n-1) x n
Contoh:
Himpunan A={1,2,3} dan himpunan B={A,B,C}. Banyaknya korespondensi satu-satu yang mungkin untuk himpunan A dan B adalah 1 x 2 x 3 = 6

Demikian rangkuman materi tentang relasi dan fungsi SMP Kelas 8 K-13. Terimakasih sudah berkunjung, dan semoga bermanfaat.