Penyelesaian Persamaan Diferensial : Eksak dan Tak Eksak
PD Eksak
Persamaan Diferensial Eksak adalah suatu PD tingkat satu dan berpangkat satu yang berbentuk
M(x, y) dx + N(x, y) dy = 0 … (i)
serta jika memenuhi
 =
=  Contoh :
Contoh :
-
y dx + x dy = 0
misal : M(x, y) = y 
 = 1
N(x, y) = x
= 1
N(x, y) = x 
 = 1
karena
= 1
karena  =
=  , maka PD diatas merupakan PD eksak.
, maka PD diatas merupakan PD eksak.
-
(2xy + ln x) dx + x2 dy = 0
misal : M(x, y) = 2xy + ln x 
 = 2x
N(x, y) = x2
= 2x
N(x, y) = x2 
 = 2x
karena
= 2x
karena  =
=  , maka PD diatas merupakan PD eksak.
, maka PD diatas merupakan PD eksak.
-
(x – y) dx + (x + y) dy = 0
misal : M(x, y) = x – y 
 = -1
N(x, y) = x + y
= -1
N(x, y) = x + y 
 = 1
karena
= 1
karena 
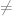
 , maka PD diatas bukan merupakan PD eksak.
, maka PD diatas bukan merupakan PD eksak.
Jika F adalah suatu fungsi dua peubah yang mempunyai derivative parsial tingkat satu yang kontinyu dalam suatu domain D, maka diferensial total fungsi F yaitu dF didefinisikan oleh
dF(x) =  dx +
dx + 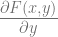 dy,
dy, 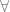 (x, y)
(x, y)  D
Misal penyelesain umum PD (i) adalah F(x, y) = C dengan C adalah konstanta sebarang, maka
dF(x, y) = 0, sedemikian sehingga
D
Misal penyelesain umum PD (i) adalah F(x, y) = C dengan C adalah konstanta sebarang, maka
dF(x, y) = 0, sedemikian sehingga
 dx +
dx + 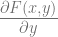 dy = 0 … (ii)
dari PD (i) dan pers (ii), diperoleh
(a)
dy = 0 … (ii)
dari PD (i) dan pers (ii), diperoleh
(a)  = M(x, y)
(b)
= M(x, y)
(b) 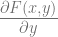 = N(x, y)
Sehingga solusi PD Eksak berbentuk F(x, y) = C. Berdasarkan hal tersebut, dapat dicari solusi PD sebagai berikut :
(a)
= N(x, y)
Sehingga solusi PD Eksak berbentuk F(x, y) = C. Berdasarkan hal tersebut, dapat dicari solusi PD sebagai berikut :
(a)  = M(x, y)
F(x, y) =
= M(x, y)
F(x, y) =  M(x, y) dx + g(y)
NOTE : bentuk
M(x, y) dx + g(y)
NOTE : bentuk  adalah integral terhadap x, dimana y dipandang sebagai konstanta dan g(y) konstanta integral yang harus dicari.
adalah integral terhadap x, dimana y dipandang sebagai konstanta dan g(y) konstanta integral yang harus dicari.
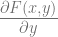 =
=  [
[ M(x, y) dx] + g'(y)
Karena
M(x, y) dx] + g'(y)
Karena 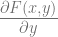 = N(x, y) maka
= N(x, y) maka
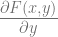 =
=  [
[ M(x, y) dx] + g'(y) = N(x, y)
g'(y) = N(x, y) –
M(x, y) dx] + g'(y) = N(x, y)
g'(y) = N(x, y) –  [
[ M(x, y) dx]
karena g'(y) merupakan fungsi dengan peubah y saja maka setelah disederhanakan merupakan fungsi dari y atau konstanta. Dengan kata lain g(y) dapat dicari
(b)
M(x, y) dx]
karena g'(y) merupakan fungsi dengan peubah y saja maka setelah disederhanakan merupakan fungsi dari y atau konstanta. Dengan kata lain g(y) dapat dicari
(b) 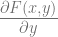 = N(x, y)
Integralkan kedua ruas terhadap variabel y, diperoleh
F(x, y) =
= N(x, y)
Integralkan kedua ruas terhadap variabel y, diperoleh
F(x, y) = 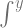 N(x, y) dy + f(x)
turunkan kedua ruas dengan turunan parsial terhadap x
N(x, y) dy + f(x)
turunkan kedua ruas dengan turunan parsial terhadap x
 =
=  [
[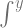 N(x, y) dy] + f'(x)
karena
N(x, y) dy] + f'(x)
karena  = M(x, y) maka
= M(x, y) maka
 =
=  [
[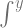 N(x, y) dy] + f'(x) = M(x, y)
f'(x) = M(x, y) –
N(x, y) dy] + f'(x) = M(x, y)
f'(x) = M(x, y) –  [
[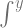 N(x, y) dy]
Contoh :
N(x, y) dy]
Contoh :
-
Cari solusi dari PD (x + y) dx + (x – y) dy = 0
Penyelesaian :
Cek terlebih dahulu apakah PD diatas adalah PD eksak.
misal : M(x , y) = x + y 
 = 1
N(x , y) = x – y
= 1
N(x , y) = x – y 
 = 1
karena
= 1
karena  =
=  , maka PD tesebut adalah PD eksak.
Untuk mencari solusinya, kita akan menggunakan
F(x, y) =
, maka PD tesebut adalah PD eksak.
Untuk mencari solusinya, kita akan menggunakan
F(x, y) =  M(x, y) dx + g(y)
=
M(x, y) dx + g(y)
=  (x + y) dx + g(y)
=
(x + y) dx + g(y)
= 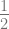 x2 + xy + g(y)
cari g'(y)
x2 + xy + g(y)
cari g'(y)
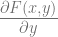 =
=  [
[ M(x, y) dx] + g'(y)
=
M(x, y) dx] + g'(y)
=  [
[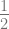 x2 + xy] + g'(y)
= x + g'(y)
karena
x2 + xy] + g'(y)
= x + g'(y)
karena 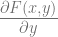 = N(x, y), maka
x + g'(y) = N(x, y)
x + g'(y) = x – y
g'(y) = -y
= N(x, y), maka
x + g'(y) = N(x, y)
x + g'(y) = x – y
g'(y) = -y
 g'(y) =
g'(y) =  -y
g(y) =
-y
g(y) =  y2
jadi solusi umumnya :
y2
jadi solusi umumnya : 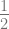 x2 + xy –
x2 + xy – 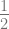 y2 = c1
x2 + 2xy – y2 = C, dengan C = 2c1
y2 = c1
x2 + 2xy – y2 = C, dengan C = 2c1
-
PD : xy’ + y + 4 = 0
Penyelesaian :
x  + y + 4 = 0
x dy + (y + 4) dx = 0
misal : M(x , y) = y + 4
+ y + 4 = 0
x dy + (y + 4) dx = 0
misal : M(x , y) = y + 4 
 = 1
N(x , y) = x
= 1
N(x , y) = x 
 = 1
karena
= 1
karena  =
=  , maka PD tesebut adalah PD eksak.
Untuk mencari solusinya, kita akan menggunakan
F(x, y) =
, maka PD tesebut adalah PD eksak.
Untuk mencari solusinya, kita akan menggunakan
F(x, y) = 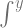 N(x, y) dy + g(x)
=
N(x, y) dy + g(x)
= 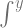 x dy + g(x)
= xy + g(x)
cari g'(x)
x dy + g(x)
= xy + g(x)
cari g'(x)
 =
=  [
[ N(x, y) dy] + g'(x)
=
N(x, y) dy] + g'(x)
=  [xy] + g'(x)
= y + g'(x)
karena
[xy] + g'(x)
= y + g'(x)
karena 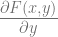 = N(x, y), maka
y + g'(x) = M(x, y)
y + g'(x) = y + 4
g'(x) = 4
= N(x, y), maka
y + g'(x) = M(x, y)
y + g'(x) = y + 4
g'(x) = 4
 g'(x) =
g'(x) =  4
g(x) = 4x
jadi solusi umumnya : xy + 4x = C
4
g(x) = 4x
jadi solusi umumnya : xy + 4x = C
y dx + x dy = 0
misal : M(x, y) = y 
 = 1
= 1
N(x, y) = x 
 = 1
= 1
karena  =
=  , maka PD diatas merupakan PD eksak.
, maka PD diatas merupakan PD eksak.
(2xy + ln x) dx + x2 dy = 0
misal : M(x, y) = 2xy + ln x 
 = 2x
= 2x
N(x, y) = x2 
 = 2x
= 2x
karena  =
=  , maka PD diatas merupakan PD eksak.
, maka PD diatas merupakan PD eksak.
(x – y) dx + (x + y) dy = 0
misal : M(x, y) = x – y 
 = -1
= -1
N(x, y) = x + y 
 = 1
= 1
karena 
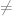
 , maka PD diatas bukan merupakan PD eksak.
, maka PD diatas bukan merupakan PD eksak.
Cari solusi dari PD (x + y) dx + (x – y) dy = 0
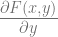 =
=  [
[ M(x, y) dx] + g'(y)
M(x, y) dx] + g'(y)
 g'(y) =
g'(y) =  -y
-y
Penyelesaian :
Cek terlebih dahulu apakah PD diatas adalah PD eksak.
misal : M(x , y) = x + y 
 = 1
= 1
N(x , y) = x – y 
 = 1
= 1
karena  =
=  , maka PD tesebut adalah PD eksak.
, maka PD tesebut adalah PD eksak.
Untuk mencari solusinya, kita akan menggunakan
F(x, y) =  M(x, y) dx + g(y)
M(x, y) dx + g(y)
=  (x + y) dx + g(y)
(x + y) dx + g(y)
= 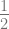 x2 + xy + g(y)
x2 + xy + g(y)
cari g'(y)
=  [
[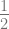 x2 + xy] + g'(y)
x2 + xy] + g'(y)
= x + g'(y)
karena 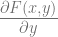 = N(x, y), maka
= N(x, y), maka
x + g'(y) = N(x, y)
x + g'(y) = x – y
g'(y) = -y
g(y) =  y2
y2
jadi solusi umumnya : 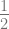 x2 + xy –
x2 + xy – 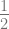 y2 = c1
y2 = c1
x2 + 2xy – y2 = C, dengan C = 2c1
PD : xy’ + y + 4 = 0
 =
=  [
[ N(x, y) dy] + g'(x)
N(x, y) dy] + g'(x)
 g'(x) =
g'(x) =  4
4
Penyelesaian :
x  + y + 4 = 0
+ y + 4 = 0
x dy + (y + 4) dx = 0
misal : M(x , y) = y + 4 
 = 1
= 1
N(x , y) = x 
 = 1
= 1
karena  =
=  , maka PD tesebut adalah PD eksak.
, maka PD tesebut adalah PD eksak.
Untuk mencari solusinya, kita akan menggunakan
F(x, y) = 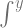 N(x, y) dy + g(x)
N(x, y) dy + g(x)
= 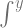 x dy + g(x)
x dy + g(x)
= xy + g(x)
cari g'(x)
=  [xy] + g'(x)
[xy] + g'(x)
= y + g'(x)
karena 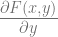 = N(x, y), maka
= N(x, y), maka
y + g'(x) = M(x, y)
y + g'(x) = y + 4
g'(x) = 4
g(x) = 4x
jadi solusi umumnya : xy + 4x = C
PD Tidak Eksak (Faktor Integral)
Persamaan Diferensial Tidak Eksak adalah suatu PD tingkat satu dan berpangkat satu yang berbentuk
M(x, y) dx + N(x, y) dy = 0 … (i)
dan memenuhi syarat
Penyelesaian PD tidak eksak dapat diperoleh dengan dengan mengalikan PD (i) dengan suatu fungsi u yang disebut Faktor Integral (FI), sehingga diperoleh PD eksak yaitu
u M(x, y) dx + u N(x, y) dy = 0 … (ii)
karena PD sudah berbentuk eksak, maka memenuhi
u  + M
+ M  = u
= u  + N
+ N 
u ( –
–  ) = – (M
) = – (M  – N
– N  )
)
RUMUS UMUM FAKTOR INTEGRAL
u(x, y) = 
Secara umum Faktor Integral terdiri dari tiga kasus yaitu
(a) FI u sebagai fungsi x saja
karena u sebagai fungsi x saja, maka
Oleh karena itu, Rumus Umum Faktor Integral diatas dapat ditulis
u(x) = 
u(x) = 
u(x) = 
dengan h(x) = 
(b) FI u sebagai fungsi y saja
karena u sebagai fungsi y saja, maka
Oleh karena itu, Rumus Umum Faktor Integral diatas dapat ditulis
u(y) = 
u(y) = 
u(y) = 
dengan h(y) = 
(c) FI u sebagai fungsi x dan y
andaikan FI : u = u(x, y)
misal bentuk peubah x, y = v
maka FI : u = u(v)
Jika pers (iii), (iv) dan (v) disubstitusikan ke RUMUS UMUM FAKTOR INTEGRAL, maka
u(x, y) = 
u(v) = 
ln u = 

Jadi, FI : u(v) = 
dengan h(v) = 
Contoh :
Tentukan Faktor Integral dan penyelesain PD dibawah ini :
- (4 xy + 3y2 – x) dx + x(x + 2y) dy = 0Penyelesaian :misal : M(x, y) = 4 xy + 3y2 – xN(x, y) = x(x + 2y)
= 4x + 6y
= 2x + 2y
Jadi,=
=[fungsi dari x saja]
maka FI adalah=
= x2
sehingga diperoleh PD eksak adalahx2 (4 xy + 3y2 – x) dx + x3 (x + 2y) dy = 0dx +
dy = 0
Karena PD diatas sudah berbentuk PD eksak, sehingga untuk mencari solusinya digunakan Penyelesaian PD Eksak.ambil= x2 (4 xy + 3y2 – x)
= 4x3y + 3x2y2 – x3F(x, y) =(4x3y + 3x2y2 – x3) dx + g(y)
= x4y + x3y2 –x4 + g(y)
= x4 + 2x3y + g'(y)
karena= G(x, y), sehingga
x4 + 2x3y + g'(y) = x3 (x + 2y)x4 + 2x3y + g'(y) = x4 + 2x3yg'(y) = 0g(y) = Csolusi PD : x4y + x3y2 –x4 + C
- y(x + y + 1) dx + x(x + 3y + 2) dy = 0Penyelesaian :misal : M(x, y) = xy + y2 + yN(x, y) = x2 + 3xy + 2x
= x + 2y + 1
= 2x + 3y + 2
Jadi,=
=[fungsi dari y saja]
maka FI adalah=
= y
sehingga diperoleh PD eksak adalahy2(x + y + 1) dx + xy(x + 3y + 2) dy = 0dx +
dy = 0
Karena PD diatas sudah berbentuk PD eksak, sehingga untuk mencari solusinya digunakan Penyelesaian PD Eksak.ambil= y2(x + y + 1)
= xy2 + y3 + y2F(x, y) =(xy2 + y3 + y2) dx + g(y)
=x2y2 + xy3 + xy2 + g(y)
= x2y + 3xy2 + 2xy + g'(y)
karena= G(x, y), sehingga
x2y + 3xy2 + 2xy + g'(y) = xy(x + 3y + 2)x2y + 3xy2 + 2xy + g'(y) = x2y + 3xy2 + 2xyg'(y) = 0g(y) = Csolusi PD :x2y2 + xy3 + xy2 + C
- (2x3y2 – y) dx + (2x2y3 – x) dy = 0Penyelesaian :misal : M(x, y) = 2x3y2 – yN(x, y) = 2x2y3 – x
= 4x3y – 1
= 4xy3 – 1
Jadi,–
= (4x3y – 1) – (4xy3 – 1)
= 4xy(x2 – y2)ambil :v = xy= y dan
= x
M= x(2x3y2 – y)
N= y(2x2y3 – x)
makaM– N
= (2x4y2 – xy) – (2x2y4 – xy)= 2x2y2(x2 – y2)=
=dv
=dv [fungsi x dan y]
maka FI adalah u(x, y) ===sehingga diperoleh PD eksak adalah(2x3y2 – y) dx +
(2x2y3 – x) dy = 0
dx +
dy = 0
Karena PD diatas sudah berbentuk PD eksak, sehingga untuk mencari solusinya digunakan Penyelesaian PD Eksak.ambil=
(2x3y2 – y)
= 2x –F(x, y) =(2x –
) dx + g(y)
= x2 ++ g(y)
=
+ g'(y)
karena= G(x, y), sehingga
+ g'(y) =
(2x2y3 – x)
+ g'(y) = 2y –
g'(y) = 2yg(y) = y2solusi PD : x2 ++ y2 = 0
No comments:
Post a Comment